



Компьютерное моделирование

Компьютерная модель - это модель реального процесса или явления,
реализованная компьютерными средствами. Если состояние системы меняется со
временем, то модели называют динамическими, в противном случае -
статическими.
Процессы в системе могут протекать по-разному в зависимости от условий, в
которых находится система. Следить за поведением реальной системы при
различных условиях бывает трудно, а иногда и невозможно. В таких случаях,
построив модель, можно многократно возвращаться к начальному состоянию и
наблюдать за ее поведением. Этот метод исследования систем называется
имитационным моделированием.
Примером имитационного моделирование может служить вычисление числа
 = 3,1415922653... методом Монте-Карло.
Этот метод позволяет определять площади и объемы фигур (тел), которые
сложно вычислить другими методами. Предположим, что требуется определить
площадь круга. Опишем вокруг него квадрат (площадь которого, как известно,
равна квадрату его стороны) и будем случайным образом бросать в
квадрат точки, проверяя каждый раз, попала ли точка в круг или нет. При
большом числе точек отношение площади круга к площади квадрата
будет стремиться к отношению числа точек, попавших в круг, к общему числу
брошенных точек.
= 3,1415922653... методом Монте-Карло.
Этот метод позволяет определять площади и объемы фигур (тел), которые
сложно вычислить другими методами. Предположим, что требуется определить
площадь круга. Опишем вокруг него квадрат (площадь которого, как известно,
равна квадрату его стороны) и будем случайным образом бросать в
квадрат точки, проверяя каждый раз, попала ли точка в круг или нет. При
большом числе точек отношение площади круга к площади квадрата
будет стремиться к отношению числа точек, попавших в круг, к общему числу
брошенных точек.
Теоретическая основа этого метода была известна давно, однако до
появления компьютеров этот метод не мог найти сколько-нибудь широкого
применения, ибо моделировать случайные величины вручную - очень трудоемкая
работа. Название метода происходит от города Монте-Карло в княжестве Монако,
знаменитого своими игорными домами, ибо одним из механических приборов
для получения случайных величин является рулетка.
Следует заметить, что данный метод вычисления площади круга будет
давать корректный результат только если точки будут не просто
случайно, но еще и равномерно разбросанными по всему квадрату.
Для моделирования равномерно распределенных в интервале от 0 до 1 случайных
чисел используется датчик случайных чисел - специальная компьютерная
программа. На самом деле эти числа определяются по некоторому алгоритму и уже
в силу этого они не являются вполне случайными. Получаемые таком способом
числа часто называют псевдослучайными. Вопрос о качестве датчиков
случайных чисел весьма непрост, однако для решения не слишком сложных задач
обычно достаточно возможностей датчиков, встроенных в большинство систем
программирования и электронных таблиц.
Заметим, что располагая датчиком равномерно распределенных случайных чисел,
генерирующим числа r из интервала [0; 1),
легко получить равномерно распределенные случайные числа на произвольном
интервале [a; b) по формуле
x=a+(b-a)*r.
Задания
1.
Разработайте модель случайного одномерного блуждания (модель "пьяницы").
Блуждание задается по правилу: если случайное число из отрезка [0;1) меньше
0,5, то делается шаг влево, в противном случае - вправо.
Для реализации модели используйте электронную таблицу. Предположим, что
в начальный момент объект наблюдения находится в точке с y-координатой
равной y0. Если случайное число больше 0,5, то
y-координата увеличивается на 1, в противном случае - уменьшается на 1.
Для наглядности процесса блуждания постройте диаграмму, отражающую
местоположение объекта. При пересчете таблицы датчики выдадут новые
последовательности чисел и траектория блуждания изменится.
На рисунках приведены две случайные траектории блуждания, вдоль
горизонтальной оси отложено число шагов.
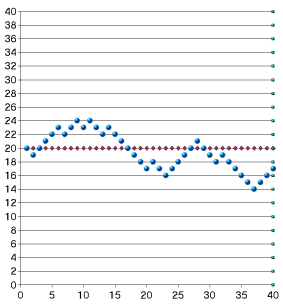
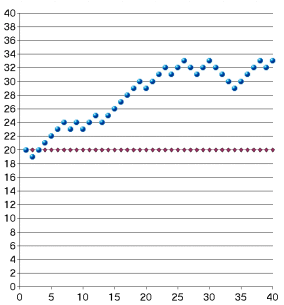 2. Постройте модель хаотического блуждания точки на плоскости с возможностью
делать шаги влево-вправо-вверх-вниз.
2. Постройте модель хаотического блуждания точки на плоскости с возможностью
делать шаги влево-вправо-вверх-вниз.



 = 3,1415922653... методом Монте-Карло.
Этот метод позволяет определять площади и объемы фигур (тел), которые
сложно вычислить другими методами. Предположим, что требуется определить
площадь круга. Опишем вокруг него квадрат (площадь которого, как известно,
равна квадрату его стороны) и будем случайным образом бросать в
квадрат точки, проверяя каждый раз, попала ли точка в круг или нет. При
большом числе точек отношение площади круга к площади квадрата
будет стремиться к отношению числа точек, попавших в круг, к общему числу
брошенных точек.
= 3,1415922653... методом Монте-Карло.
Этот метод позволяет определять площади и объемы фигур (тел), которые
сложно вычислить другими методами. Предположим, что требуется определить
площадь круга. Опишем вокруг него квадрат (площадь которого, как известно,
равна квадрату его стороны) и будем случайным образом бросать в
квадрат точки, проверяя каждый раз, попала ли точка в круг или нет. При
большом числе точек отношение площади круга к площади квадрата
будет стремиться к отношению числа точек, попавших в круг, к общему числу
брошенных точек.






