Пределы и ряды

Пределы и ряды

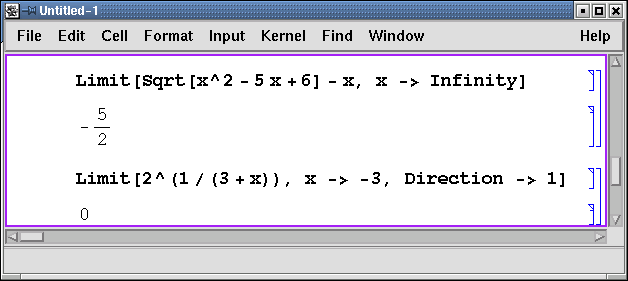
Для вычисления пределов используется функция Limit. Необязательный параметр Direction применяется для вычисления односторонних пределов, которые используют, в частности, при исследовании функции на непрерывность.
Внимание: Direction -> 1 является указанием для вычисления предела слева, а Direction -> -1 - для предела справа.

Константа Infinity обозначает бесконечность, для ее ввода в виде символа

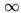можно использовать палитру Basic Input.

Не все пределы могут быть вычислены таким образом. Дополнительные возможности предоставляет пакет расширений Calculus, подпакет Limit которого переопределяет встроенную функцию Limit. Для загрузки используется команда

<<Calculus`Limit`

Пример
Следующий предел может быть найден только с использованием указанного модуля расширений.

Limit[Cos[n!]/n, n -> Infinity]

Пример
Используем односторонние пределы для исследования функции на непрерывность. Напомним, что функция называется непрерывной в точке x, если она определена в ней и ее значение в этой точке совпадает с левым и правым пределами функции при стремлении к x. Точка x является точкой устранимого разрыва, если пределы слева и справа существуют (принимают конечные значения) и равны, но значение функции f(x) не существует или отлично от них. Точка x называется точкой разрыва первого рода, если пределы не совпадают, но конечны. Наконец, x есть точка разрыва второго рода, если в ней не существует хотя бы одного конечного предела.

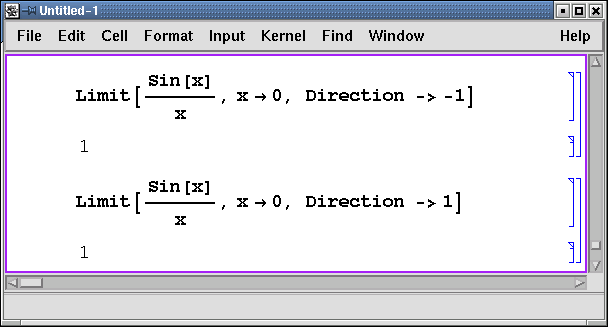
Для функции sin(x)/x точка x = 0 является точкой устранимого разрыва, так как существуют пределы слева и справа, равные 1.

Довольно часто в процессе решения различных задач математического анализа приходится сталкиваться с рядами и разложением аналитических функций в ряды. Поэтому в программе Mathematica имеется обширный набор функций для решения подобного рода проблем. Для получения частичной суммы ряда используется функция Sum[f, {i, imin, imax}]. Здесь f - общий член ряда, а imin и imax - границы суммирования.

Большинство достаточно гладких функций довольно точно локально аппроксимируются рядом Тейлора. Для нахождения n-го многочлена Тейлора в окрестности точки x0 применяется функция Series[f, {x, x0, n}], а удаление остаточного члена ряда выполняется функциями Collect и Normal:

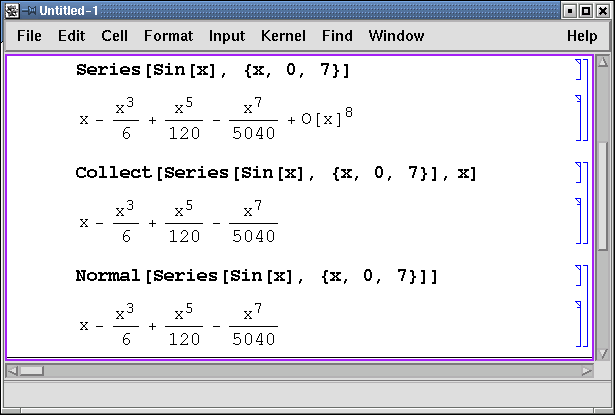
Пример
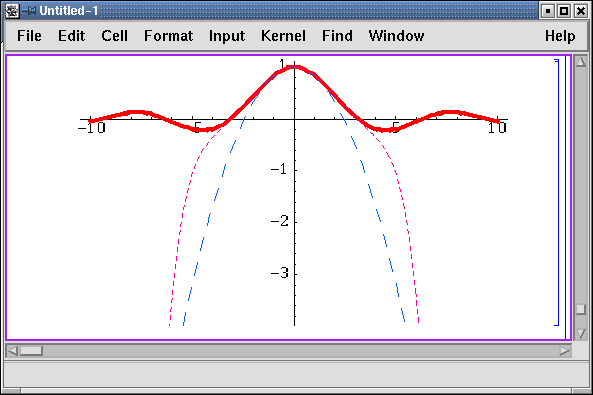
Для того чтобы наглядно представить себе точность апроксимации функции многочленами Тейлора, построим на одном рисунке график функции sin(x)/x и соответствующие ей многочлены Тейлора степеней 3 и 6.

f=Sin[x]/x;
f1= Normal[Series[f, {x, 0, 3}]];
f2= Normal[Series[f, {x, 0, 6}]];
Plot[{f, f1, f2}, {x, -10, 10}, 
  PlotStyle -> {
     {Hue[0], Thickness[.01]},
     {Hue[.6], Dashing[{.03}]},
     {Hue[.9], Dashing[{.01}]}}]

Задания

Вычислите пределы:
а) ; б) .
Найдите односторонний предел .
Исследуйте функции на непрерывность:
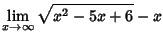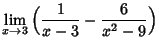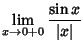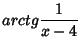а) ; б) 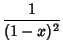.